CONTENTS
1. Critical Thinking Principles
5. Evaluating Deductive Reasoning

Credit: Portland Community College, STEM Center
1. Critical Thinking Principles

CTP Index |
1 - 2 Logical possibility
3 - 4 Physical possibility
5 - 6 Personal experience
7 - 9 Belief vs. knowledge
10 - 11 Background information
12 - 15 Evidence / experts for claims
16 - 18 Objective reality
19 - 21 Scientific method / hypotheses
22 - 26 Criteria of adequacy for hypotheses
CTP List (1) |
| 1. Whatever is logically impossible is simply not possible (and can never be real). Consider the law of non-contradiction: Nothing can both have a property and lack it at the same time. For example, one cannot be a bachelor and married at the same time. A binary state cannot be both 1 and 0 at the same time. Note that this principle applies to the macrocosmic world of human experience, and not necessarily at the quantum scale. |
| 2. Just because something is logically possible doesn’t mean that it’s real. Our universe is governed by physical laws and whatever violates them cannot occur. Hence, although it’s logically possible for a cow to jump over the moon (nothing in the concept of 'cow' makes a 'flying cow' a contradiction), it is not physically possible because of scientific laws relating to gravity and bovine physiology. (Note that many sci-fi creations are simply beings that are currently considered physically impossible.) |
| 3. Just because something seems physically impossible doesn’t mean that it is. As our knowledge of the physical world increases, our understanding of the limits of physical possibility expands. For example, Einstein believed that quantum entanglement of particles—"spooky action at a distance," as he called it—is not physically possible. But we now know that this seemingly impossible phenomenon is real. |
| 4. Just because something is physically possible doesn’t mean that it’s real
Possibility does not imply actuality. To establish that something is real, we need reliable evidence that it actually exists. Pictures used to be reliable visual evidence of some state of affairs in the world. Now we must be able to determine the integrity, source, and context for an image before we can give it the status of "evidence." |
| 5. Just because something seems (feels, appears) real doesn’t mean that it is.
We can’t infer what is from what seems. It is an error in reasoning to conclude that an event or phenomenon (X) is real because it seems real. Questions to ask: Is my experience of X corroborated or shared by others? Does my experience of or conclusion about X contradict all known previous experience? Is it possible that a peculiarity of human perception / cognition (eg: color constancy), could be operative? |
| 6. It’s reasonable to accept personal experience as reliable evidence only if there is no reason to doubt its reliability.
Reasons for doubting include: perceptual construction, memory construction, effects of stress, effects of expectancy and belief, selective attention, misjudgments of probabilities, subjective validation, altered states of consciousness, poor observational conditions, sensory impairments or limitations, and conflicts with other observations / knowledge that we have good reason to believe. |
| 7. Just because you believe that something is true doesn’t mean that it is.
We can’t make something true simply by believing it to be true. The early Greek philosopher Protagoras (c. 490 – c. 421 BCE) held that "man is the measure of all things." Today, this subjectivist notion of truth can be seen in statements like "Well, this is my truth, and that’s your truth." Subjective truths are not the same as objective truths. |
| 8. Just because a group of people believe that something is true doesn’t mean that it is.
As an extension of individual subjectivism, social relativism holds that society, not the individual, determines what is true. But, society used to believe that the Earth was flat, that the sun orbited the Earth, etc. The same problems and contradictions that plague individual subjectivism also aflict social relativism. |
| 9. We are justified in believing a proposition when we have no good reason to doubt it.
Neither knowledge nor reasonable belief requires certainty. Practical wisdom takes note of probabilities. A proposition is beyond a reasonable doubt when it provides the best explanation of something. But being justified in believing a proposition is no guarantee of its truth. |
| 10. There is good reason to doubt a proposition if it conflicts with other propositions that we have good reason to believe. The quest for knowledge involves eliminating inconsistencies and contradictions among our beliefs. Sometimes we observe or learn about things that conflict with our background knowledge—that vast system of well-supported beliefs that we habitually use to guide our thoughts and actions (much of it referred to as "common sense"). Background knowledge includes both "street smarts" and "school smarts." |
| 11. The more a proposition conflicts with background information, the more reason there is to doubt it.
The structure of background information can be compared to the structure of a large tree. Bigger branches (beliefs) support smaller ones, which in turn support even smaller ones. Accepting some claims is analogous to pruning small branches—giving up only peripheral beliefs. Accepting others is akin to cutting large branches. |
| 12. Just because a claim hasn’t been conclusively refuted doesn’t mean that it’s true. The truth of a claim is established by the amount and type of evidence in its favor—not by the lack of evidence against it. Also, attempting to place the burden of proof on the nonbeliever is asking for the impossible. To prove a universal negative statement (eg: No X things exist.), you would have to exhaustively investigate all of time and space. |
| 13. Just because a claim hasn’t been conclusively proven doesn’t mean that it’s false.
This is the "flip side" of the preceding principle. Here again, the error in reasoning is an appeal to ignorance as in this example: "No one has ever proven that alternate universes exist; therefore they don’t". |
| 14. When there is good reason to doubt a proposition, we should proportion our belief to the evidence.
The more evidence we have for a proposition, the more credence we should give it. The probability of the truth of a contingent or scientific proposition can range from close to 0 (eg: Someday, humans will travel faster than the speed of light.), to close to 1 (eg: E = mc 2). It is generally held that only logical truths warrant such strong belief that their probability values equal 1 (eg: "The bar is either one meter long or it isn’t.") |
| 15. There is good reason to doubt a proposition if it conflicts with expert opinion.
The opinions of experts are superior to our own, but only in their fields of expertise. Just because someone is an expert in one field doesn’t mean that he or she is an expert in another. For example, being an accomplished actor or skillful athlete does not make a person qualified to offer medical opinions. |
| 16. If we have no reason to doubt what’s disclosed to us through perception, introspection, memory, or reason, then we are justified in believing it.
Only if we have good reason for believing that they are not functioning properly should we doubt the traditional sources of knowledge: perception (the physical senses), introspection (witnessing dispositional mental states), memory, and reason. |
| 17. Rational discourse assumes a search or quest for objective truth.
When there is disagreement about a particular state of affairs, the objectivist (moderate realist), believes that it is at least theoretically possible to determine truths through rational discourse. Humans syndicate confidence in their common beliefs through ongoing dialogue with each other, and through the methods of logic and science. |
18. It is possible that "normal" consciousness may not provide the best perspective from which to view reality.
|
| 19. The scientific method is self-correcting, and as a result, our most reliable method for determining the truth of the physical world.
The scientific method is our most reliable means of establishing the truth of an empirical proposition beyond a reasonable doubt. Science seeks to understand the world by identifying general principles that are both explanatory and predictive. To minimize the potential for error, inadequacy, or fraud, the scientific method requires repeatable results. In general, any procedure that serves to systematically eliminate reasonable grounds for doubt can be considered scientific. For example, consider this general method:
|
| 20. Hypotheses are created, not discovered.
The process of creating hypotheses (possible explanations) is just as open-ended as the process of artistic creation. Although inductive reasoning can lead to the formulation of a hypothesis, other processes—like direct insight, and imaginative construction—are also sources of useful hypotheses. A good hypothesis must account for all the evidence it is intended to explain. |
| 21. A hypothesis is scientific only if it is testable—that is, if it predicts something other than what it was introduced to explain.
If a hypothesis cannot be tested, there is no way to determine whether it is true or false. Hypotheses have observable consequences only in the context of a background theory. So, to be testable, a hypothesis must predict something more than what is already assumed by the background theory. |
| 22. Other things being equal, the best hypothesis is the one that is the most fruitful. Some hypotheses are attractive because they promise to open new lines of research by making the most novel predictions. For example, Einstein’s theory of relativity predicts that light waves travelling near massive objects will appear to be bent because space-time around these bodies is curved. Before Einstein, the common belief was that light traveled in Euclidean straight lines since photons had no mass. |
| 23. Other things being equal, the best hypothesis is the one that has the greatest scope. The more a hypothesis explains and predicts, the more it systematizes and unifies our knowledge. For example, Einstein’s theory of relativity came to be preferred over Newtonian theories of gravity and motion because the theory of relativity explained and predicted everything that Newton’s theories could, plus some things that it couldn’t (like variations in Mercury’s orbit). |
| 24. Other things being equal, the best hypothesis is the simplest one.
(Occam’s Razor)
Although not simple to define, scientific simplicity can be understood as the fewest number of assumptions required by a hypothesis. The simpler the hypothesis, the more it unifies and systematizes our knowledge, and the less likely it is to be false since there are fewer ways for it to go wrong. Hence, Copernicus’s heliocentric theory of planetary motion was considered preferable to Ptolemy’s geocentric theory. This principle is often referred to as Occam’s Razor: Do not multiply entities beyond necessity. |
| 25. Other things being equal, the best hypothesis is the most conservative one. The hypothesis that fits best with established beliefs is to be preferred. It might be reasonable to accept a hypothesis that is not conservative if it possesses other criteria of adequacy. There are borderline cases where reasonable people can disagree, and clear-cut cases where disagreement would be irrational. Although it may not be clear at what point a person becomes bald, it's irrational to consider a person with a full head of living hair as bald. |
| 26. We should accept an extraordinary hypothesis only if no ordinary one will suffice. The criteria of simplicity and conservatism should lead you to prefer ordinary explanations over unusual and ad hoc (created after the emergence of the phenomena) explanations. You should always reject any explanation for which no possible evidence could count against it—where every apparent counterexample is explained away or not allowed to count. |
2. Critical Thinking Overview
2.1 Core Critical Thinking Skills
2.2 FAIR Assessment Engine
2.3 Integrative Learning & Thinking
2.4 Fast & Slow Thinking
"The experts find good critical thinking to include both a skill dimension and a dispositional dimension. The experts find CT to include cognitive skills in:
(1) interpretation,
(2) analysis,
(3) evaluation,
(4) inference,
(5) explanation, and
(6) self-regulation.Each of these six is at the core of CT. "
– Peter A. Facione
SKILL Dimension: Consensus List of Core CT Cognitive Skills and Sub-Skills (2) |
1. INTERPRETATION |
Sub Skills: Categorization, Decoding Significance, Clarifying Meaning |
2. ANALYSIS |
| Sub Skills: Examining Ideas, Identifying Arguments, Analyzing Arguments To identify the intended and actual inferential relationships among statements, questions, concepts, descriptions, or other forms of representation intended to express beliefs, judgments, experiences, reasons, information, or opinions. |
3. EVALUATION |
Sub Skills: Assessing Claims, Assessing Arguments |
4. INFERENCE |
| Sub Skills: Querying Evidence, Conjecturing Alternatives, Drawing Conclusions
To identify and secure elements needed to draw reasonable conclusions; to form conjectures and hypotheses; to consider relevant information and to educe the consequences flowing from data, statements, principles, evidence, judgments, beliefs, opinions, concepts, descriptions, questions, or other forms of representation. |
5. EXPLANATION |
Sub Skills: Stating Results, Justifying Procedures, Presenting Arguments
|
6. SELF-REGULATION |
| Sub Skills: Self-examination, Self-correction
Self-consciously to monitor one's cognitive activities, the elements used in those activities, and the results educed—particularly by applying skills in analysis and evaluation to one's own inferential judgments with a view toward questioning, confirming, validating, or correcting either one's reasoning or one's results. |
As is evident, particularly in the descriptions of self-examination and self-correction, there are dispositional components to critical thinking. Indeed each cognitive skill, if it is to be exercised appropriately, can be correlated with the cognitive disposition to do so. – Peter A. Facione
DISPOSITIONAL Dimension: Consensus List of Core CT Affective Dispositions (2) |
APPROACHES TO LIFE AND LIVING IN GENERAL |
|
APPROACHES TO SPECIFIC ISSUES, QUESTIONS OR PROBLEMS |
■ clarity in stating the question or concern ■ orderliness in working with complexity ■ diligence in seeking relevant information ■ reasonableness in selecting and applying criteria ■ care in focusing attention on the concern at hand ■ persistence though difficulties are encountered ■ precision to the degree permitted by the subject and the circumstance
|
Skeptical habits of thought are essential...for nothing less than our survival because baloney, bamboozles, bunk, careless thinking, flimflam, and wishes disguised as facts are not restricted to parlor magic and ambiguous advice on matters of the heart. – Carl Sagan

If you are confused by claims about stuff like fake news, UFO reports, Big Foot sightings, ESP, conspiracy reports, etc., then use this "engine" to uncover the baloney. This tool is a general method for rigorously evaluating unusual or weird claims that you might encounter. This "engine" has four cycles or steps—similar to a four-cycle internal combustion engine. But this "engine" is just a method —you are the thinker!
| |
| 1. Formulate the unusual claim. This is the "intake" cycle. Some of this input, or claims, might be stated in vague or incomplete ways. So the first step is to formulate all claims so that they are as clear and specific as possible. Note: Although not all claims are hypotheses, any unusual claim can be considered a hypothesis—a provisional explanation for a particular phenomenon.or state of affairs. |
| 2. Analyze the evidence for the claim. This is the "compression" cycle. At this point you put the claim under the pressure of your analysis of the evidence or reasons that are put forward to support it. You will use the critical thinking principles outlined in the CTP List. |
| 3. Identify alternative hypotheses. This is the "combustion" cycle. Now, you let your creative imagination and critical intelligence explode into other possible ways to explain the phenomenon in question. |
| 4. Rate each hypothesis. This is the "exhaust" cycle. You eliminate all hypotheses that fail the criteria of adequacy. Only the most robust hypothesis remains—generating new or more refined understanding. |
1. FORMULATE THE UNUSUAL CLAIM.
► INTAKE
Note that although not all claims are hypotheses, any unusual claim can be considered a hypothesis—a provisional explanation for a particular phenomenon. Before you examine any unusual claim, you must first be sure that it is stated clearly, with specific rather than general, vague, or ambiguous terms. For example, the claim "Astrology is true" is vague. This claim could be taken to mean that a field of "study" called astrology exists. To avoid these kinds of ambiguities, you would need to recast this claim into something like: "Astrologers can correctly identify someone's personality traits and predict personal future events by using sun signs." Although this is an improvement on the original claim, an even more exact formulation will be more specific about what it means to "correctly identify someone's personality traits" and "predict personal future events."
2. ANALYZE THE EVIDENCE FOR THE CLAIM.
► COMPRESSION

What are the reasons — empirical evidence or logical arguments — for accepting the unusual claim / hypothesis? Use the Critical Thinking Principles (CTP List) to guide you through the 3-D analysis process:
|
■ Determine the exact nature and limitations of the empirical evidence. |
■ Discover if any of these reasons (pieces of evidence) should be disqualified. |
■ Decide whether the hypothesis (claim) in question explains (accounts for) all the evidence. |
3. INDENTIFY ALTERNATIVES.
► COMBUSTION
The quest for truth requires an open mind. Whether or not you have disqualified a particular claim in cycles 1 and 2 above, it is always prudent to consider if there are other ways (hypotheses), to account for the phenomena in question.. So, in this cycle, you use your creativity to compose alternative explanations. You should continue looping through cycles 1 - 3 until you have identified all plausible alternatives.
4. RATE EACH HYPOTHESIS.
► EXHAUST
Finally, after exploring credible, alternative hypotheses, you must evaluate each according to the criteria of adequacy (CTP #22 – 26). By applying these criteria to all candidate hypotheses, you should be able to quickly eliminate some and reduce the field to only one or two or three possibilities—depending on how many alternatives you identified in cycle 3. Following CTP #14, the more evidence you have for a proposition, the more credence you should give it. So, the more that a particular hypothesis meets all the criteria of adequacy better than any other alternative, the more it deserves to be considered the best explanation so far.
Integrative learning is the process of making connections among concepts and experiences so that information and skills can be applied to novel and complex issues or challenges. (Ithaca College, 2019) Integrative Critical Thinking (ICT) employs the concepts, theories, and methods of logic for addressing topics, issues, problem areas, or human challenges that currently confront us or are likely to emerge in the future. ICT will help you analyze new questions and complex problems, and it will support you in developing habits of self-reflection and self-assessment. Fast and Slow Thinking is the title of a landmark book by
Daniel Kahneman that summarizes his pioneering research over many years.
Dr. Kahneman describes two different ways the human brain forms thoughts: System 1 (Fast thinking), and System 2 (Slow thinking). System 1 is FAST, automatic, frequent, emotional, stereotypic, unconscious. Examples of System 1's abilities include: System 2 is SLOW, effortful, infrequent, logical, calculating, conscious. Examples of System 2's abilities include:
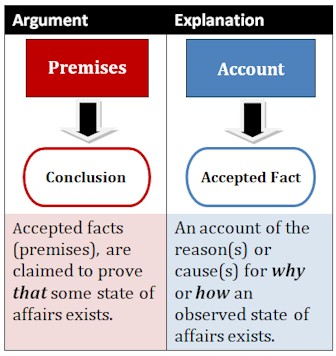
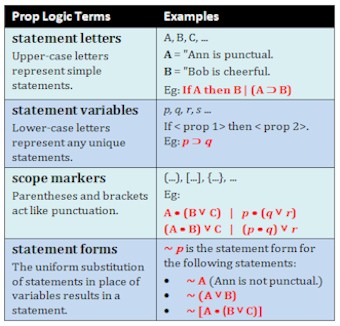
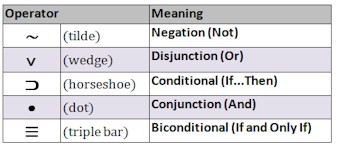
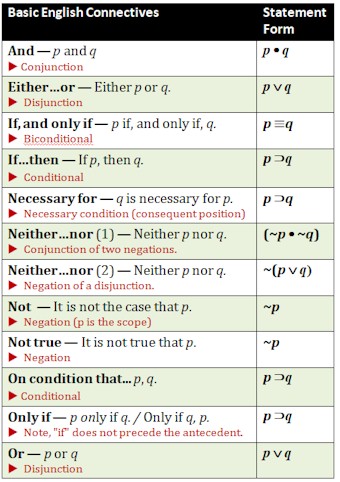
3.1 Logic Overview Logic is the organized body of knowledge, or science, that evaluates arguments. As the science that evaluates arguments, the aim of logic is to develop methods and techniques that enable us to distinguish good arguments from bad ones. Among the benefits to be expected from the study of logic is an increase in confidence that we are making sense when we criticize the arguments of others and when we advance arguments of our own. argument A group of statements, one or more of which (the premises) are claimed to provide support for, or reasons to believe, one of the others (the conclusion). Every argument may be placed in either of two basic groups: those in which the premises really do support the conclusion (good arguments), and those in which they do not, even though they are claimed to (bad arguments). statement A sentence that is either true or false, typically a declarative sentence or a sentence component that could stand as a declarative sentence. The following sentences are statements: In this guide, proposition and statement are used synonymously. proposition In the narrow sense, the meaning or information content of a statement. Technically, the three statements: "The pig is big." | "Le cochon est gros." | "El cerdo es grande." express a single proposition. In this guide, proposition and statement are used synonymously. truth values Truth (T) and falsity (F) are called the two possible truth values of a statement. premise(s) The statement(s) that set forth the reasons or evidence for the conclusion. conclusion The statement that is claimed to follow from (supported by or inferred from) the premises. inference In the narrow sense of the term, the reasoning process expressed by an argument. In the broad sense of the term, “inference” is used interchangeably with “argument.” deductive argument An argument incorporating the claim that it is impossible for the conclusion to be false given that the premises are true. inductive argument An argument incorporating the claim that it is improbable that the conclusion is false given that the premises are true. Regardless of the type of argument, whether deductive or inductive, the evaluation of any argument involves answering two distinct questions: The answer to the first question is the more important one, because if the premises fail to support the conclusion (that is, if the reasoning is bad), the argument is worthless. Any statement following one of these indicators can usually be identified as a premise: Any statement following one of these indicators can usually be identified as a conclusion: simple
non-inferential
passages Passages (texts) that lack a claim that anything is being proved. Such passages contain statements that could be premises or conclusions (or both), but what is missing is a claim that any potential premise supports a conclusion or that any potential conclusion is supported by premises. Passages of this sort include: expository passage A kind of discourse that begins with a topic sentence followed by one or more sentences that develop the topic sentence. If the objective is not to prove the topic sentence but only to expand it or elaborate it, then there is no argument illustration An expression involving one or more examples that is intended to show what something means or how it is done. Often confused with arguments because many illustrations contain indicator words such as “thus". explanation An expression that purports to shed light on some event or phenomenon. The event or phenomenon in question is usually accepted as a matter of fact. Every explanation is composed of two distinct components: the explanandum and explanans. The explanandum (accepted fact) is the statement that describes the event or phenomenon to be explained, and the explanans (the account of reasons) is the statement or group of statements that purports to describe the causes for the occurance of the event or phenomenon. An argument intends to establish that some state of affairs is the case. An explanation intends to establish why or how some state of affairs is the case: In some cases, a text or passage can be considered as both an argument and explanation. Extended arguments often describe the causes or reasons for the existence of the particular phenomena they intend to prove to be real. conditional statement an “if… then…” statement; for example: • If professional football games incite violence in the home, then the widespread approval given to this sport should be reconsidered. antecedent The component statement immediately following the “if”. consequent The component statement immediately following the “then”. The link between the antecedent and consequent resembles the inferential link between the premises and conclusion of an argument. Yet there is a difference because the premises of an argument are claimed to be true, whereas no such claim is made for the antecedent of a conditional statement. Accordingly, conditional statements are not arguments. necessary condition If A then B. B is said to be a necessary condition for A. Thus, being an animal is a necessary condition for being a dog. sufficient condition If A then B. A is said to be a sufficient condition for B. For example, being a dog is a sufficient condition for being an animal. The relation between conditional statements and arguments can be summarized:
4.1 Deductive Argument Forms Argument based on mathematics An argument based on mathematics is an argument in which the conclusion depends on some purely arithmetic or geometric computation or measurement. For example, a shopper might place two apples and three oranges into a paper bag and then conclude that the bag contains five pieces of fruit. Or a surveyor might measure a square piece of land and, after determining that it is on each side, conclude that it contains . Since all arguments in pure mathematics are deductive, we can usually consider arguments that depend on mathematics to be deductive as well. However, arguments that depend on statistics are a noteworthy exception and are usually best interpreted as inductive. argument from definition an argument in which the conclusion is claimed to depend merely on the definition of some word or phrase used in the premise or conclusion. For example, someone might argue that because Claudia is mendacious, it follows that she tells lies, or that because a certain paragraph is prolix, it follows that it is excessively wordy. These arguments are deductive because their conclusions follow with necessity from the definitions of “mendacious” and “prolix.” syllogism In general, an argument consisting of exactly two premises and one conclusion. categorical syllogism Each statement in a categorical syllogism begins with one of the words “all,” “no,” or “some.” All As are Bs. hypothetical syllogism A syllogism having a conditional (“if… then”) statement for one or both of its premises. If p then q. disjunctive syllogism A syllogism having a disjunctive (“either… or…”) statement. Either p or q. categorical proposition A proposition that relates two classes, or categories. The classes are denoted respectively by the Subject (S) term and the Predicate (P) term. The proposition asserts that either all or part of the class denoted by S is included in or excluded from the class denoted by P. standard form The standard-form of a categorical proposition is: Eg: All S are P A, E, I, and O propositions The names of the four types of categorical propositions: All S are P. No S are P. Some S are P. Some S are not P. distribution Universal (A and E) statements distribute their subject terms. Negative (E and O) statements distribute their predicate terms. Briefly: Universals distribute Subjects, and Negatives distribute Predicates. So, A statements distribute the Subject, E statements distribute both terms, I statements distribute neither term, and O statements distribute the Predicate. Venn diagram Each circle is labeled so that it represents one of the terms in the proposition. In general, the left-hand circle represents the subject (S) term, and the right-hand circle the predicate (P) term. Aristotelian standpoint From the Aristotelian standpoint the first two universal propositions (A and E) can convey evidence about existence. When things exist, the Aristotelian standpoint recognizes their existence, and universal statements about those things have existential import. Boolean standpoint From the Boolean standpoint, the first two universal propositions (A and E) imply nothing about the existence of the things denoted by S. When things exist, the Boolean standpoint does not recognize their existence, and universal statements about those things have no existential import. interpreting universal propositions The Aristotelian and Boolean standpoints are alternative sets of "ground rules" for interpreting the meaning of universal propositions. Either standpoint can be adopted for any categorical proposition or any argument composed of categorical propositions. Venn Diagrams: Shading = emptiness | X = existence All S are P (universal) No members of S are outside P. Aristotelian Standpoint: Existence implied if referring to actually existing things (real beings). Boolean Standpoint: Existence not implied. No S are P (universal) No members of S are inside P. Aristotelian Standpoint: Existence implied if referring to actually existing things (real beings). Boolean Standpoint: Existence not implied. Some S are P (particular) At least one S exists that is a P. The word “some” implies existence. Eg: “Some mammals are zebras” asserts that at least one mammal exists that is a zebra. Some S are not P (particular) At least one S exists that is not a P. The word “some” implies existence. Eg: “Some mammals are not zebras” asserts that at least one mammal exists that is not a zebra. categorical syllogism A deductive argument that has three categorical propositions and is able to be translated into standard syllogistic form. class complement | term complement The complement of a class is the group consisting of everything outside the class. For example, the complement of the class of dogs is the group that includes everything that is not a dog (cats, fish, trees, and so on). The term complement is the word or group of words that denotes the class complement. For terms consisting of a single word, the term complement is usually formed by simply attaching the prefix “non” to the term. Thus, the complement of the term “dog” is “non-dog,” the complement of the term “book” is “non-book,” and so on. form of a syllogism The form of a syllogism is determined by its mood and figure. After a categorical syllogism has been put into standard form, its validity or invalidity can be determined by merely inspecting its form. mood Denoted by the letter names (A, E, I, O), of its constituent propositions. The letter for the major premise is listed first, then the letter for the minor premise, and finally the letter for the conclusion. figure Determined by the position of the occurrences of the middle term in the premises. There are four figures: For example: No cyborgs are Earthlings. Some Earthlings are Martians. Therefore, some Martians are not cyborgs. In this example, the term Earthlings is the middle term. So, this syllogism is in Figure 4. An EIO-4 categorical argument is always valid. See section 5.2 below for more information. The traditional Square of Opposition depicts the Aristotelian standpoint. Opposite truth value At least one is false At least one is true 5.1 Validity & Soundness valid deductive argument An argument in which it is impossible for the conclusion to be false given that the premises are true. In these arguments the conclusion follows with strict necessity from the premises. invalid deductive argument A deductive argument in which it is possible for the conclusion to be false given that the premises are true. In these arguments the conclusion does not follow with strict necessity from the premises, even though it is claimed to. test for validity To test an argument for validity we begin by assuming that all the premises are true, and then we determine if it is possible, in light of that assumption, for the conclusion to be false. A deductive argument that is valid and has all true premises. Both conditions must be met for an argument to be sound; if either is missing the argument is unsound. A sound argument, therefore, is what is meant by a good, or successful, deductive argument in the fullest sense of the term. It is not always possible to determine the soundness of a deductive argument. But that does not mean that soundness is unimportant in logic. It is crucially important that soundness be recognized as a criterion of evaluation that is distinct from validity. A deductive argument that is invalid, has one or more false premises, or both. Different syllogistic figures produce valid arguments for different moods. But note that some moods (eg: EIO) produce valid arguments in more than one figure. Consider the following EIO categorical syllogism: No cyborgs are Earthlings. Some Earthlings are Martians. Therefore, some Martians are not cyborgs. Because this syllogism has the form of EIO-4 (mood EIO + figure 4 ), it is a valid argument. In categorical logic, the fundamental elements are terms (subjects and predicates). In propositional (Prop) logic, the fundamental elements are whole statements (propositions). Statements are represented by letters, and these letters are combined with operators or connectives to symbolize compound statements. By symbolizing the statements in an argument, it is much easier to evaluate the shape or form of an argument and quickly determine its validity. Truth Tables for Logical Operators Valid Forms Arguments with the following forms are always valid. That is, it is impossible for their conclusions to be false if their premises are in fact true. Invalid Forms Arguments with the following forms are always invalid. Note that these corrupt forms are errors in using the forms modus ponens and modus tollens. 6.1 Inductive Argument Forms strong inductive argument An inductive argument in which it is improbable that the conclusion be false given that the premises are true. In such arguments, the conclusion does in fact follow probably from the premises. weak inductive argument An inductive argument in which the conclusion does not follow probably from the premises, even though it is claimed to. uniformity of nature All inductive arguments depend on the principle that the future tends to replicate the past, and regularities that prevail in one spatial region tend to prevail in other regions. Good inductive arguments are those that accord with the uniformity of nature. They have conclusions that we naturally expect to turn out true. test for strength To test an inductive argument for strength we begin by assuming that all the premises are true, and then we determine whether, based on that assumption, the conclusion is probably true. This determination is accomplished by linking up the premises with regularities that exist in our experiential background. All of these regularities are instances of the uniformity of nature. cogent argument A is an inductive argument that is strong and has all true premises. Also, the premises must be true in the sense of meeting the total evidence requirement. If any one of these conditions is missing, the argument is uncogent. A cogent argument is the inductive analogue of a sound deductive argument and is what is meant by a good, or successful, inductive argument without qualification. uncogent argument An inductive argument that is weak, has one or more false premises, fails to meet the total evidence requirement, or any combination of these defects. 7.1 Language and Meaning types of meaning Linguistic expressions can have different kinds of meaning: emotive meaning Statements having emotive meaning often make value claims. When such statements occur in arguments, the value claims should be disengaged from the emotive terminology and expressed as separate premises. value claim A claim that something is good, bad, right, wrong, better, worse, more important, or less important than some other thing. Such value claims are often the most important part of the cognitive meaning of emotive statements. cognitive meaning Cognitive meanings can be defective in two ways: Ambiguity and vagueness are important in logic because there are countless occasions in which the evaluation of an argument leads to the observation, “Well, that depends on what you mean by …” If phraseology in an argument is vague or ambiguous, its meaning must be clarified before any evaluation can proceed. vague expression An expression that allows for borderline cases in which it is impossible to tell if the expression applies or does not apply. Vague expressions often allow for a continuous range of interpretations. The meaning is hazy, obscure, and imprecise. How fresh does something have to be in order to be called “fresh”? ambiguous expression An expression that can be interpreted as having more than one clearly distinct meaning in a given context. For example, if one were to describe a beer as a light pilsner, does this mean that the beer is light in color, light in calories, or light in taste? term A word or phrase that can serve as the subject of a statement. Terms include: intension Intensional meaning of a term refers to the attributes that the term connotes. For example, the intensional meaning of the term “cat” consists of the attributes of being furry, of having four legs, of moving in a certain way, of emitting certain sounds, etc. conventional connotation The conventional connotation of a term includes the attributes that the term commonly calls forth in the minds of competent speakers of the language. The connotation of a term remains more or less the same from person to person and from time to time. extension Extensional meaning of a term refers to the members of the class that the term denotes. The extensional meaning of the term “cat” consists of cats themselves—all the cats in the universe. empty extension Terms with empty extension denote the empty (or “null”) class, the class that has no members. For example, “unicorn,” “leprechaun,” “gnome,” “elf,” and “griffin.” mention (of a word) "Wherever" is an eight-letter word.” In this statement, it is not the word itself that is the subject but rather the quoted word. In this statement, “wherever” is mentioned. use (of a word) “I will follow you wherever you go.” In this statement, “wherever” is used. Many forms of expression are ambiguous in one context and vague in another. For example, the word “slow” in one context could mean either mentally challenged or physically slow, but when the word refers to physical slowness, it could be vague. How slow is slow? definition A word or group of words that assigns a meaning to a word or group of words: Definitions can serve different purposes, so there are different kinds of definitions Stipulative definitions Assign a meaning to a word when it first comes into use. This may involve either coining a new word or giving a new meaning to an old word. The purpose of a stipulative definition is usually to replace a more complex expression with a simpler one. Because a stipulative definition is a completely arbitrary assignment of a meaning to a word for the first time, there can be no such thing as a “true” or “false” stipulative definition. Lexical definitions Report the meaning a word has within a community of users. Dictionary definitions are all instances of lexical definitions. In contrast with a stipulative definition, which assigns a meaning to a word for the first time, a lexical definition may be true or false depending on whether it does or does not report the way a word is actually used. Also, lexical definitions are useful for eliminating ambiguity. Precising definitions Reduce the vagueness of a word. The definition “‘Poor’ means having an annual income of less than $10,000 and a net worth of less than $20,000” is an example of a precising definition. Whenever words are taken from ordinary usage and used in a highly systematic context such as science, mathematics, medicine, or law, they must always be clarified by means of a precising definition. Theoretical definitions Appeal to a theory to characterize whatever the term denotes. Such a definition provides a way of viewing or conceiving these entities that suggests deductive consequences, further investigation (experimental or otherwise), and whatever else would be entailed by the acceptance of a theory governing these entities. The definition of the term “heat” found in texts dealing with the kinetic theory of heat is a good example: “‘Heat’ means the energy associated with the random motion of the molecules of a substance.” Many terms in philosophy, such as “substance,” “form,” “cause,” “change,” “idea,” “good,” “mind,” and “God,” have been given theoretical definitions. Persuasive definitions Influence the attitudes of the community of users regarding whatever the word denotes. Persuasive definitions amount to a certain synthesis of stipulative, lexical, and, possibly, theoretical definitions backed by the rhetorical motive to engender a certain attitude. As a result of this synthesis, a persuasive definition masquerades as an honest assignment of meaning to a term while condemning or blessing with approval the subject matter of the definiendum. For example: definition by genus and difference 8.1 Cognitive Bias "A cognitive bias is a systematic pattern of deviation from norm or rationality in judgment. Individuals create their own "subjective reality" from their perception of the input. An individual's construction of reality, not the objective input, may dictate their behavior in the world. Thus, cognitive biases may sometimes lead to perceptual distortion, inaccurate judgment, illogical interpretation, or what is broadly called irrationality." (3) When stupid people think they're smart, they do maximum damage. Ignorance can easily lead to arrogance. In many areas of life, incompetent people do not recognize — scratch that, cannot recognize — just how incompetent they are, a phenomenon that has come to be known as the Dunning-Kruger effect. Logic itself almost demands this lack of self-insight: For poor performers to recognize their ineptitude would require them to possess the very expertise they lack. To know how skilled or unskilled you are at using the rules of grammar, for instance, you must have a good working knowledge of those rules, an impossibility among the incompetent. Poor performers — and we are all poor performers at some things — fail to see the flaws in their thinking or the answers they lack. What's curious is that, in many cases, incompetence does not leave people disoriented, perplexed, or cautious. Instead, the incompetent are often blessed with an inappropriate confidence, buoyed by something that feels to them like knowledge. (4) Starter List for Antiracist Reading A fallacy is a defect in an argument that arises from a mistake in reasoning or the creation of an illusion that makes a bad argument appear good. The term non sequitur (“it does not follow”) is another name for fallacy. Both deductive and inductive arguments may contain fallacies; if they do, they are either unsound or uncogent, depending on the kind of argument. Fallacies are usually divided into two groups: Fallacies that occur in real-life argumentation may be hard to detect: Three factors underlie the commission of fallacies in real-life argumentation: An informal fallacy is a defect in an argument that can be detected only by examining the content of the argument. Consider the following example: My house is made of atoms. To detect this fallacy one must know something about houses—namely, that they are large visible objects, and even though their atomic components are invisible, this does not mean that the houses themselves are invisible. Since the time of Aristotle, logicians have attempted to classify the various informal fallacies. Here is a useful way to classify common informal fallacies: Fallacies of Relevance The premises are not relevant to the conclusion. Fallacies of Weak Induction: The premises may be relevant to the conclusion, but they supply insufficient support for the conclusion. Fallacies of Presumption: The premises presume what they purport to prove. Fallacies of Ambiguity: The conclusion depends on some kind of linguistic ambiguity. Fallacies of Illicit Transference: An attribute is incorrectly transferred from the parts of something onto the whole or from the whole onto the parts. Accident A general rule is applied to a specific case it was not intended to cover. Appeal to force Arguer threatens the reader/listener. Appeal to pity Arguer elicits pity from the reader/listener. Appeal to the people Arguer incites a mob mentality (direct form) or appeals to our desire for security, love, or respect (indirect form). This fallacy includes appeal to fear, the bandwagon argument, appeal to vanity, appeal to snobbery, and appeal to tradition. Argument against the person Arguer personally attacks an opposing arguer by: Missing the point Arguer draws a conclusion different from the one supported by the premises. Red herring Arguer leads the reader / listener off the track (with a misleading scent). Straw man Arguer distorts an opponent’s argument and then attacks the distorted argument. Appeal to ignorance Premises report that nothing is known or proved about some subject, and then a conclusion is drawn about that subject. Appeal to unqualified authority Arguer cites an untrustworthy authority. False cause Conclusion depends on a nonexistent or minor causal connection. This fallacy has four forms: Hasty generalization A general conclusion is drawn from an atypical sample. Slippery slope Conclusion depends on an unlikely chain reaction of causes. Weak analogy Conclusion depends on a defective analogy (similarity). Begging the question Arguer creates the illusion that inadequate premises are adequate by leaving out a key premise, restating the conclusion as a premise, or reasoning in a circle. Complex question Multiple questions are concealed in a single question. False dichotomy An “either … or …” (disjunctive) premise hides additional alternatives. Suppressed evidence Arguer ignores important evidence that requires a different conclusion. Equivocation Conclusion depends on a shift in meaning of a word or phrase. Amphiboly Conclusion depends on an incorrect interpretation of an ambiguous statement made by someone other than the arguer. ► Incorrect attribution from parts to whole or from whole to parts: Composition An attribute is incorrectly transferred from the parts to the whole. Division An attribute is incorrectly transferred from the whole to the parts.
■ determine that an object is at a greater distance than another
■ brace yourself before the start of a sprint
3. Logic Basics
3.2 Argument Basics
3.3 Argument Premise Indicators
3.4 Argument Conclusion Indicators
3.5 Non-Arguments
3.6 Arguments vs. Explanations
3.7 Conditional Statements

![]() Concepts
Concepts
• Melatonin helps relieve jet lag.
• Politicians always tell the complete truth.
• No wives ever cheat on their husbands.
• Tiger Woods plays golf and Maria Sharapova plays tennis.
since
as a result
consequently
entails that
for this reason
hence
implies that
it follows that
it must be that
so
therefore
thus
we may conclude
we may infer
wherefore
![]() Concepts
Concepts
![]() Analyzing Extended Arguments
Analyzing Extended Arguments
![]() Concepts
Concepts
• If Roger Federer has won more Grand Slams than any other contender, then he rightfully deserves the title of world’s greatest tennis player.
Summary of Conditional Statements vs. Arguments
4. Deductive Logic
4.2 Categorical Propositions
4.3 Categorical Syllogisms
4.4 Square of Opposition
![]() Concepts
Concepts
All Bs are Cs
Therefore, all As are Cs.
p.
Therefore, q.
Not p.
Therefore, q.
![]() Concepts
Concepts
A
E
I
O
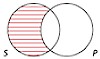
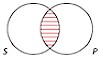
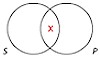
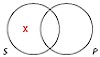
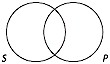 An arrangement of overlapping circles in which each circle represents the class denoted by a term in a categorical proposition. Every categorical proposition has exactly two terms (S and P), so the Venn diagram for a single categorical proposition consists of two overlapping circles.
An arrangement of overlapping circles in which each circle represents the class denoted by a term in a categorical proposition. Every categorical proposition has exactly two terms (S and P), so the Venn diagram for a single categorical proposition consists of two overlapping circles.
![]() Using Venn Diagrams
Using Venn Diagrams
![]() Concepts
Concepts
.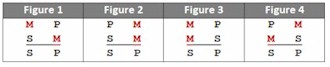
Standard Form: Categorical Syllogism

![]() How to Symbolize Categorical Syllogisms
How to Symbolize Categorical Syllogisms
To symbolize the four syllogistic figures:
Determining the figure (positions of the three terms):
.
S
the Subject of the conclusion (minor term)
P
the Predicate of the conclusion (major term)
M
the middle term (occurs once in each premise but not in the conclusion)
Determining the mood (pattern of the A, E, I, O propositions):
.
A
All S are P (universal)
E
No S are P (universal)
I
Some S are P (particular)
O
Some S are not P (particular)
Syllogisms with these figures and corresponding moods are all valid:
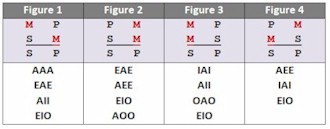
major term: cyborgs
middle term: Earthlings
middle term: Earthlings
minor term: Martians

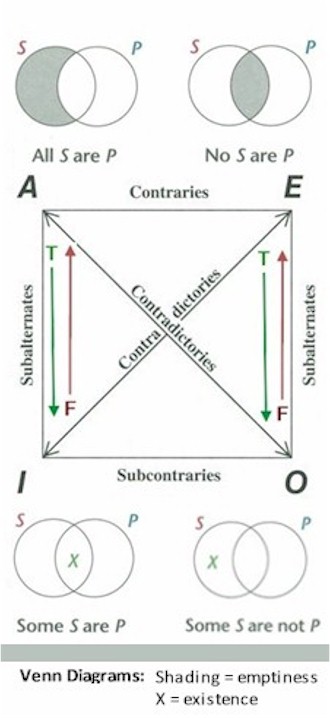
Contradictory
(the same as in the Modern Square of Opposition)
Contrary
(not both true)
Subcontrary
(not both false)
Subalternation
5. Evaluating Deductive Reasoning
5.2 Valid Categorical Syllogisms
5.3 Prop Logic: Basic Symbols
5.4 Prop Logic: Valid Inference Forms
5.5 Prop Logic: Formal Fallacies
![]() Concepts
Concepts
![]()

major term: cyborgs
minor term: Martians
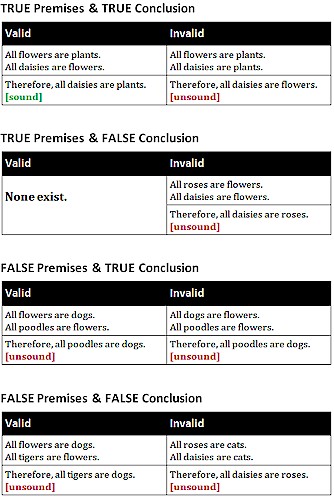
Distinguish between Sound and Unsound Arguments
(Connectives in Compound Statements)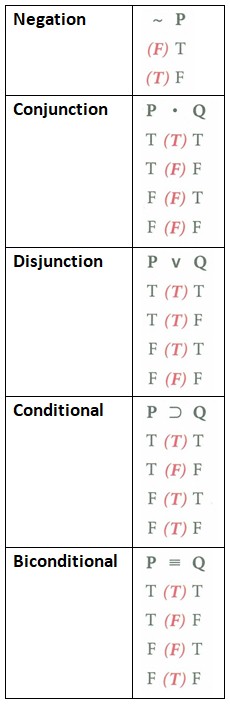
NOTE: Premises are listed first and separated by a line from the conclusion. 
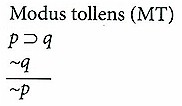
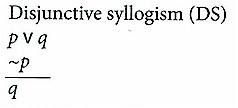


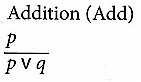
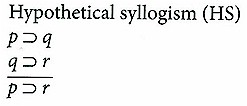
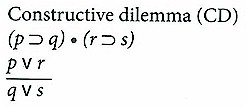

6. Inductive Logic
6.2 Evaluating Inductive Arguments
![]() Concepts
Concepts
![]()
Distinguish between Cogent and Uncogent Arguments

7. Language
7.2 Vagueness and Ambiguity
7.3 Definitions
![]() Concepts
Concepts
(connation)
(denotation)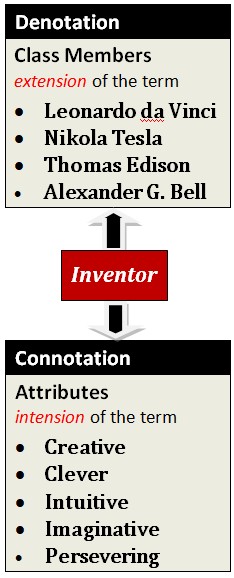
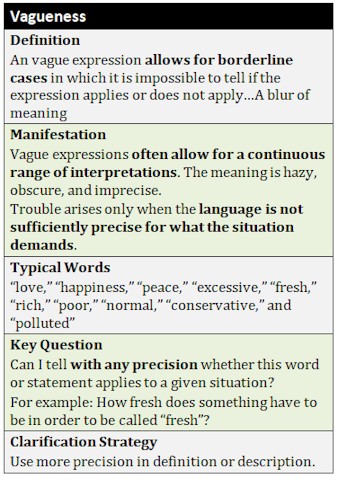

![]() Concepts
Concepts
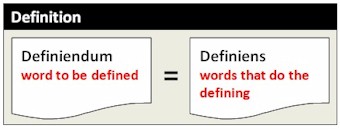
![]() How to construct definitions by genus and difference
How to construct definitions by genus and difference
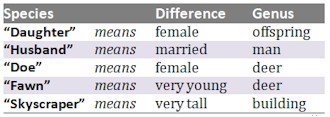
For example:
8. Bias & Fallacies
8.2 Systemic Racism
8.3 Fallacies
8.4 Common Informal Fallacies

— https://www.facebook.com/NowThisNews/videos/2745368975685853/
►Robin DiAngelo
White Fragility: Why It’s So Hard for White People to Talk About Racism
https://robindiangelo.com/publications/
►Ijeoma Oluo
So You Want to Talk About Race
https://www.indiebound.org/book/9781580058827
►Ibram X. Kendi
How to Be An Antiracist; Stamped from the Beginning: The Definitive History of Racist Ideas in America
https://www.ibramxkendi.com/stamped-from-the-beginning
►Resmaa Menakem
My Grandmother’s Hands: Racialized Trauma and the Pathway to Mending Our Hearts and Bodies
https://www.resmaa.com/books
►Ta-Nehisi Coates
Between the World and Me
https://ta-nehisicoates.com/books/between-the-world-and-me/
►Chris Crass, Roxanne Dunbar-Ortiz (forward), and Chris Dixon (introduction)
Towards Collective Liberation: Anti-Racist Organizing, Feminist Praxis, and Movement Building Strategy
https://www.pmpress.org/index.php?l=product_detail&p=518
►bell hooks
Killing Rage: Ending Racism
https://us.macmillan.com/books/9780805050271
Informal fallacies
Atoms are invisible.
Therefore, my house is invisible.
![]() Concepts
Concepts
► The premises are not relevant to the conclusion:
Fallacies of Relevance
Note: For this fallacy to occur, there must be two arguers.
Note: Do not cite this fallacy if another fallacy fits.
Note: For this fallacy to occur, there must be two arguers.
► The premises offer insufficient support for the conclusion:
Fallacies of Weak Induction
► The premises presume what they purport to prove:
Fallacies of Presumption
► The conclusion depends on some kind of linguistic ambiguity:
Fallacies of Ambiguity
Fallacies of Illicit Transference
LogicRef Gallery

Credit: Anonymous

Credit: Anonymous

Credit: Unknown

Credit: Anonymous

Credit: Roz Chast. "The Mind-Body Problem," The New Yorker, April 3, 2017.
▀
Credit: Anonymous
Credit: Anonymous

Credit: Unknown